Interpretable ML (linear regression, GAMs-generalized additibe model, Explainable boosting machine, generalized linear models)
오늘 작성할 내용은 Interpretable ML과 explainable AI이고, 그 중 interpretable ML에 관하여 설명하고자 한다.
Interpretable ML은 ML 자체가 이해가 가능한 모델로,
→ 생각보다 우리가 흔히 쓰는 linear model, logistic model 등이 포함된다.
Explainable AI란 deep neural network의 경우 성능은 잘 나오지만 왜 잘 나오는진 설명 불가능한 black box 영역이 있다. 이 blackbox 영역을 AI기법을 활용하여 설명 불가능한 영역에 설명가능한 모델을 만들도록 해주는 기법이다.
→ 알려진 AI 모델로는 SHAP, LIME, DeepLIFT 등이 있다.
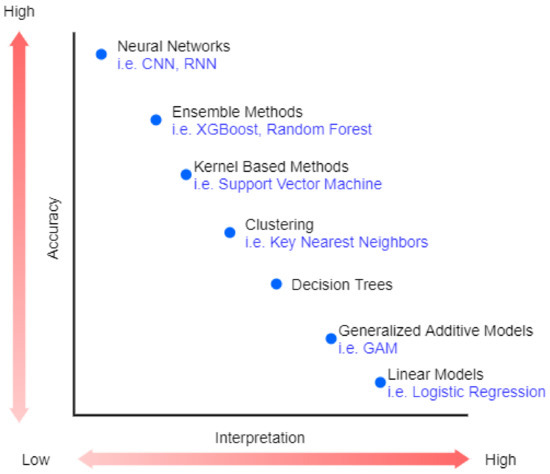
위 그림 ML/AI 모델마다 accuracy 정도와 interpretation를 그림으로 잘 나타낸 것이다.
Linear model과 같이 간단한 모델일 수록 accuracy는 낮지만, deep learning 모델로 갈 수록 accuracy는 높아지지만 interpretation은 떨어지는 것을 볼 수 있다.
그렇다면 Interpretable ML에는 어떤 종류들이 있을까?
- Linear model
- Generalized linear model (e.g logistic regression)
- Generalized additive models (GAMs)
- Explainable boosting machines (EBMs)
Linear regression
간단한 Linear Regression에 대해 먼저 살펴보자
우리는 linear regression에 대해서 수 없이 많이 들었지만, 생각보다 어떤 계산 과정으로 나오는 모델인지 모른다.
1) Linear regression 수식에 대해 먼저 이해해보자
Linear regression은 각 feature에 weight값 곱해진 것의 합이다.
- B : feature의 weight 값/ coefficients
- x : feature
- epsilon : 오차값
2) 그렇다면 위와 같은 weight값은 어떤 과정을 통해 나올까?
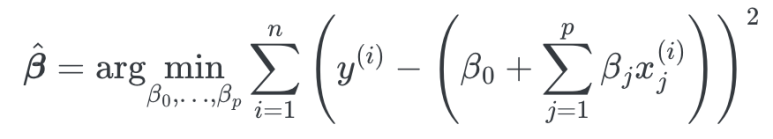
weight값을 구하기 위한 식은 다음과 같다.
weight값을 구하기 위해선 실제 y값과 estimated y값의 차이가 최소화되는 것을 통해 weight값은 지정된다.
3) Linear regression이 데이터를 얼마나 잘 설명했느냐는 R-square 값을 통해 알 수 있다.
R-square 값이 클 수록 data를 잘 설명하는 모델로, R-square값은 linear regression의 여러 오차 지표를 통해 얻어지게 된다.
오차 지표에는 SSE(Sum of Squares Residual error), SST(Sum of Squares Regression) 등이 있다.
SST :데이터 평균에서 얼만큼 떨어져 있는지의 합
SSE : linear regression line에서 데이터가 얼마나 떨어져 있는가의 합

R-square의 계산식은 아래와 같다.
따라서 SSE가 작을 수록, 데이터가 linear regression 선과 가까울 수록 R-square값은 커지게 된다.

4) Linear regression의 feature importance 구하는 법

linear regression의 feature importance를 계산하고 싶은 경우 t-static을 써서 계산하면 된다.
Generalized Linear Models
e.g logistic regression
Generalized linear model, 보편화된 linear model이란 뭘까?
우리의 삶에선 다양한 데이터 형태를 가지고 있는데,
전국 인구의 키 분포로 나타내면 -> 정규분포(gaussian) 로 표현 될 수 있고,
전국 인구의 안경 여부의 분포는 -> 0,1로 베르누이(bernolli)분포를 이룬다.
Linear regression만으로는 모든 형태의 분포를 설명 할 수 없기에
Linear regression을 변형시킨 logistic regression과 같은 generalized linear model을 생성하여 쓸 수 있다.
아래의 표는 데이터의 분포에 따른 모델의 변형 수식을 나타낸 것이다.
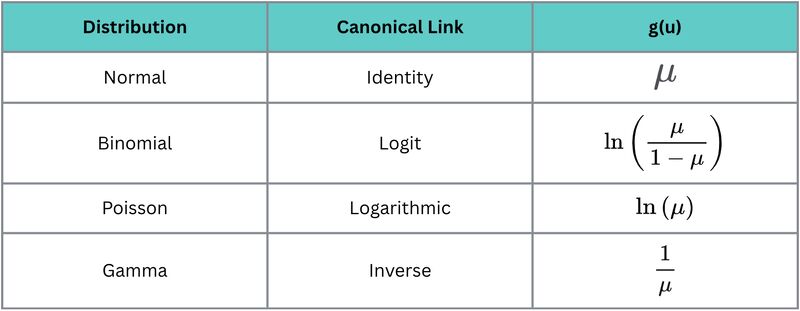
데이터가 binomial(0,1로 구성)된 경우 logit을 취하여 regression의 결과로 나온 것을 확률로 변형하여 log를 취해 0,1로 나오게 만드는 것이다.
Generalized Additive Models
Generalized additive model은 비선형 방식으로 데이터를 설명하는 것이다.
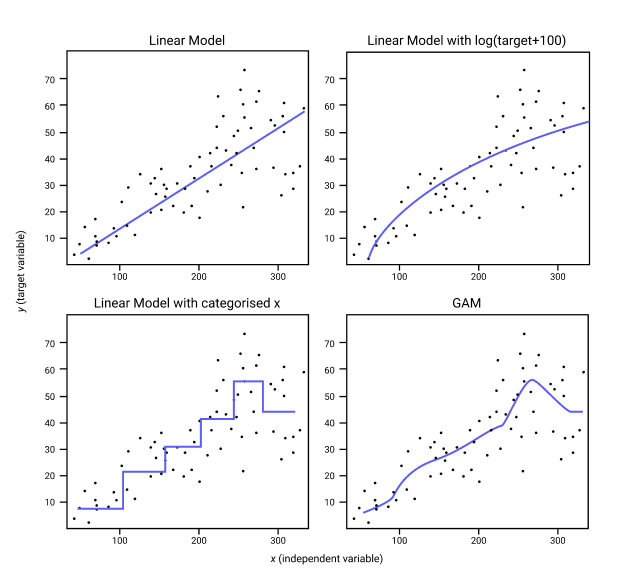
그림과 같이 linear model은 데이터를 선형적으로,
GAM은 각각의 feature들의 function을 더한 것으로 구불구불하게 전반적인 데이터를 설명할 수 있다.
수식은 다음과 같다.
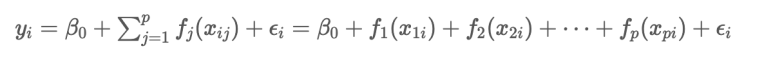
Generalized addive model의 수식이다
Linear regression과 수식은 비슷하지만, 다른 점은 각 feature마다 function을 취해 더한다는 특징이 있다.
각 feature의 function을 더하기 때문에 additive라 칭한다.
- pyGAM tool을 사용하면 됨.
Explainable Boosting Machines (EBMs)
Explainable boosting machine은 Generalized additive model의 확장 버전으로,
GAM 방식에 boosting machine function을 취하는 모델 이다.
Microsoft에서 개발한 모델로, 정확도와 interpretable을 모두 잡은 모델 중 하나이다.

Explainable boosting machine의 수식은 다음과 같다.
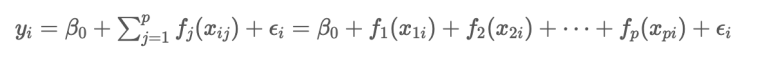
어디서 본 것 같지 않은가?
위의 generalized additive model 수식과 동일하다!
다만 다른 점은 function이 tree 구조 즉 boosting 모델이란 점이다.
그렇다면 학습 과정은 어떻게 이뤄질까?
feature1에 대한 tree function 거침 -> 여기서 residual (실제값 - 예측값) 모델의 오류가 발생 -> 이 residual을 가지고 또 tree function을 거침 -> ... 이 과정이 반복된다.
- 그렇다면 왜 residual을 가지고 계속 학습을 시키는 것일까?
그것은 모델이 틀린 예측값을 보정해주기 위해 계속해서 틀린 값을 가지고 학습을 시키는 것이다.
계속해서 residual을 보정함을 통해 오류를 줄여나가는 것이다.
from interpret.glassbox import ExplainableBoostingClassifier
from interpret import show
# 학습
ebm = ExplainableBoostingClassifier()
ebm.fit(X_train, y_train)
# 예측
preds = ebm.predict(X_test)
# 해석
show(ebm.explain_global()) # 전체 feature들의 영향 시각화
show(ebm.explain_local(X_test[0:5])) # 특정 예측에 대한 설명

