지난 글에선 MCMC에서 Monte Carlo에 해당하는 rejection sampling에 대해서 알아보았다. 이번 글에선 markov chain을 이해하는 시간을 통해 Event들이 발생했을 때 특정 결과로 어떻게 도달하는지 알아보고자 한다.
Monte Carlo에 대해서 먼저 이해가 필요하다면
https://blog.naver.com/happip_jh/223356350170 글을 먼저 보고 오면 된다.
Marcov chain을 가장 이해하기 쉬운 방법은 그림을 통해서 기본 용어 개념에 대해 익숙해지는 것이다.
■ Basic Marcov Chain
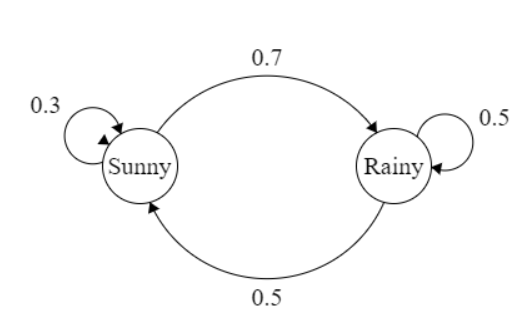
사진 설명을 입력하세요.
Marcov chain에서 나타나는 기본 개념 용어 state space, marcov assumption, transition matrix에 대해 먼저 알아보자

사진 설명을 입력하세요.
- 그림 예시를 통해 세 용어를 익혀보면 state space는 상태에 대한 공간을 나타낸 것으로 현재는 비가 오는 상태, 맑은 상태 2가지 상태가 존재한다.
- Transition matrix, 맑음 → 맑음, 맑음 → 비, 비 → 맑음, 비 → 비 4가지 전이 상태에 대한 확률을 matrix으로 표현한 것이다.
- Markov assumption, markov chain의 개념을 알 수 있는 것으로 과거의 이력을 통해 현재의 확률을 유추한다는 것으로 왼쪽의 P값은 쌓인 과거의 확률들을 통해 현재의 확률을 아는 것이다. 결과적으로 전에 상태를 통해 현재 상태 확률 아는 것을 목적을 둔다.
■ Marcov Chain 성질 : irreducible, aperiodic
위의 기본적인 marcov chain을 통해 과거의 데이터(확률)들을 통해 현재 state 확률을 알아내는 것이란 것을 이해했을 것이다. 그렇다면 어떤 수식 과정을 통해 현재 state를 알게 되는 것일까?
문제를 풀기 전에 marcov chain의 성질(용어)를 이해함을 통해 어떤 식으로 결과값을 얻어내는지 이해하고자 한다. 먼저 알아야하는 성질들은 Irreducible, aperiodic으로, 이 두 조건이 만족하게 되면 확률들이 하나의 값으로 모이면서 값을 구할 수 있게 된다.
- Irreducible : 특정 어떤 상태에서 다른 상태로 이동 할 수 있음을 의미
- Aperiodic : 상태의 반복의 주기가 모두 달라, 같은 출발선의 상태에서 같은 상태로 돌아오는데 충분한 시간이 걸림을 의미
두 성질을 이해하기 위해 두가지 case를 통해 알아보도록 하자
● 첫번째 case는 irreducible, aperiodic한 경우이다.

정답은 어느 날인지는 모르겠지만 알 수 있다! 이다.
그렇다면 어떻게 알 수 있는 것일까?
다음과 같은 계산 과정을 통해 구할 수 있다

맑음에 도달할 확률과 비가 온다에 도달할 확률의 전체 합이 1이고, 맑음 → 맑음 + 비 → 맑음 = 맑음이라는 두 수식을 만들어 계산해 맑음과 비에 대한 확률을 구할 수 있다. 위의 수식은 행렬로 만들어 역행렬을 통해 구할 수 있다.
따라서 marcov chain은 다음과 같은 확률을 특정 값에 도달하는 과정을 통해 구하게 된다. ⇒ Irreducible
|
X0
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
|
|
P(xt= S)
|
1
|
0.3
|
0.44
|
0.412
|
0.4176
|
0.4165
|
0.4167
|
0.4176
|
|
P(xt=R)
|
0
|
0.7
|
0.56
|
0.588
|
0.5824
|
0.5835
|
0.5833
|
0.5833
|
첫번째 case는 aperiodic한 것으로 매일 매일 비가 올 확률, 맑을 확률이 다르긴 하지만 최종적으론 특정 확률로 상태가 확정됨이 결정된다. ⇒ aperiodic
● 두번째는, irreducible하지만 periodic한 특징을 가진 case이다
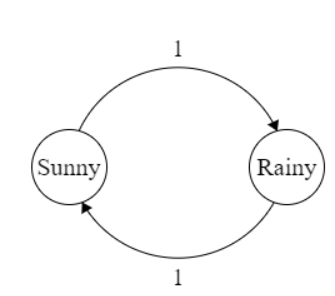
위의 그림과 다른 점이 뭘까?
|
X0
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
|
|
P(xt= S)
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
|
P(xt=R)
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
바로 periodic하다는 성질을 가지고 있는다는 점이다.
aperiodic과 반대로 위의 case는 매일매일이 지나도 0,1 주기가 반복하는 특정 확률로 고정되지 않고 있지있다. ⇒ periodic
몇일이 지나서 맑음일지 비가 올지의 확률값은

수식을 통해 알 수 있다는 irreducible한 특징을 가지고 있다.
MCMC 샘플들은 irreducible하고 aperiodic한 성질을 통해 marcov chain방법으로 값을 찾아가는 과정이라 볼 수 있다.
지금까지 Monte Carlo의 rejection sampling과 Marcov chain의 성질과 특징에 대해 총 정리해보았다.