최근에 machine learning 관련 수업을 들으면서 처음 알게된 meta learning 모델
적은 데이터만으로도 충분히 훈련 가능한 모델로 deep learning과는 또 다른 강점을 가진 모델로
meta learning이 어떤 모델인지, 수학적인 정의, 어떤 데이터에 어떻게 쓰이고 강점이 무엇인지 정리하며 meta learning의 개념에 대해 정리해 보았다.
1. 먼저 meta learning을 왜 써야 되는지 이해하고 넘어가자.
Deep learning의 경우 모델을 학습시키고 나면 fine tuning을 통해 최적의 initial parameter과 learning rate값을 찾아야 한다. 그러나 Meta learning의 경우엔 data adaptation 과정을 통해 최적의 initial parameter 값을 찾아줘 더 빠르게 학습하고 더 좋은 학습 성능을 가진다는 장점을 가진다.
모델에서의 adaptation에 대한 개념은 뒤에서 작성해 놓았다.
2. Deep learning의 한계 : Big Data
하나의 task에 대해서만 학습에 대한 결과를 내어주고 수많은 데이터가 있어야 학습 성능이 높은 모델을 만들 수 있다는 단점이 있다. 그러나, Meta learning의 경우 여러 개의 task의 적은 데이터를 가지고 있어도 훈련 가능하고, 다른 task에 대한 test에 대한 예측 결과를 내어 준다.
⇒multi-task & less data (few shot learning)
* few shot learning : 적은 데이터로 훈련하는 것
아래의 그림을 통해 model adaptation과 함께 meta learning의 정의와 가까워져 보자.
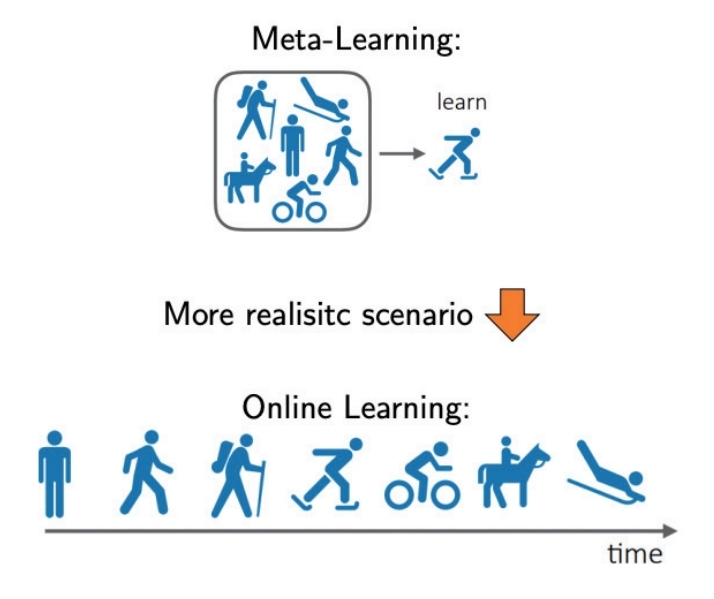
박스안에 그림처럼 수영,등산, 걷기, 말타기, 바이킹 등을 잘하는 사람은 스케이트도 잘탄다라는 가설을 세울 수 있다. meta learning 모델도 이와 비슷하게 수영/등산/걷기/말타기/바이킹과 같이 여러가지 task를 학습시켜 새로운 task 스케이트가 왔을 때도 결과를 예측 한다 라고 비유적으로 이해하면 쉽다.
⇒ 그래서 붙여진 "learning to learn" 이전의 데이터로부터 학습해 새로운 것을 학습한다!
previous data를 활용해 학습하는 meta learning 외에도 이전 경험 데이터를 활요하는 여러 모델들이 있다.
1. continuous learning
2. domain adaptation : label이 없는 데이터를 대신해 label이 많은 다른 domain 데이터(source data)를 학습시켜 target domain에 적용하는 모델
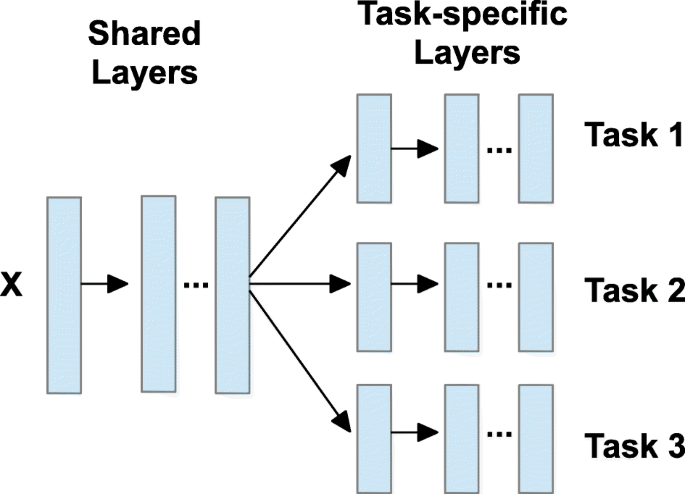
3. multi-task learning: 서로 연관 있는 task들을 동시에 훈련해 수행 능력을 향상시키는 모델
그럼 본격적으로 meta learning의 input data 형식은 어떻게 되고, 훈련은 어떻게 되는지에 대해 이해해보자.
Meta learning input data 형식
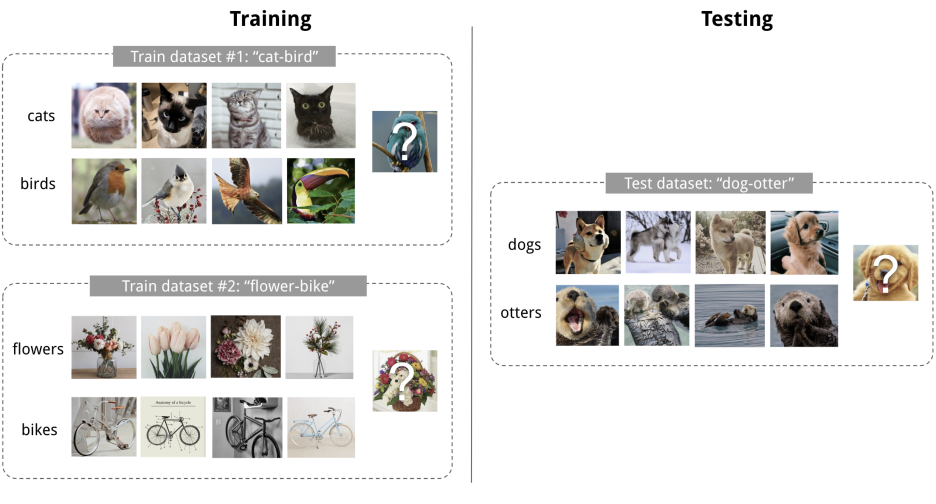
Dataset는 training에 해당하는 support set S와 prediction set에 해당하는 B가 존재한다 (D = <S,B>).
세부적으로 training dataset에는 여러개의 task가 few shot classification task로 나눠져 있는데 n-way k-shot learning으로 n개의 클래스 개수와 k의 클라스당 데이터 갯수를 의미한다.
예를 들어, 위의 Train dataset #1 cat - bird처럼 2개의 class가 있고, 각 class당 4개의 사진이 있으므로 2way 4shot learning이라 할 수 있다.
Meta learning definition & training
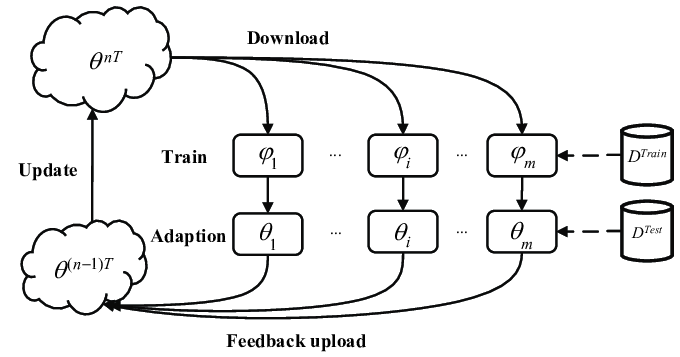
meta learning의 algorithm에 대해 이해해보도록 하자, 이전에 많이 나오는 기호들의 의미들을 알고 해석하면 더 수월하다.

meta learning의 경우 모델은 아무 model이나 사용가능하다, 먼저 dataset에 있는 task의 수식을 들여다 보면,
▶ task에 대한 정의
T ={L(x1,a1,...,xH,aH) , q(x1) , q(xt+1|xt,at), H}
→ 다양한 수식에 복잡해 보이지만 집중해서 볼 부분은 q(x1), q(xt+1|xt, at) 이다. 데이터의 x값이 q(x1)일 때, q(x1+1|xt, at) 조건부 확률의 classifier q(x1+1| xt) 를 갖고 at는 likelihood로 성능을 측정한 measure값이다.
⇒ 단순하게 말하면 그냥 training data를 data는 확률 classifier은 조건부확률로 나타낸 것이라 생각하면 된다.
▶ 최적의 parameter에 대한 정의
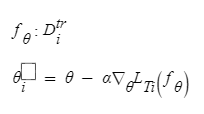
→ meta learning을 통해 최적의 parameter값을 찾아가게 되는데, 함수 f에 대해 input training data(Dtr)이 들어가게 되고 gradient descent 방식을 통해 최적의 parameter값 θ을 찾아가게 된다. 이 parameter값을 통해 model에 들어가 예측 값을 뱉어나는 과정을 하게 거치게 된다.
⇒ 최적의 parameter를 찾아가는 과정을 "adaptation"라 칭한다.
▶ classifier에 대한 정의
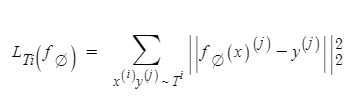
→ 앞서 구한 parameter값을 위의 공식에 대입하여, 정답값과 예측값을 MSE로 비교하면서 오차를 줄여가는 식으로 test data에 대한 예측값을 찾아가는 과정이다.