통계 공부를 했던 사람이라면 ' 어제 오늘 비가 올 확률이 70%로 라면 내일 비가 안 올 확률은?' 와 같은 문제를 marcov chain monte carlo방법으로 접근해 푸는 것을 한번쯤은 본 기억이 있을 것이다.
그래서 오늘은 어렴풋이 알았던 MCMC(marcov chain monte carlo)의 rejection sampling의 개념에서부터 MCMC가 문제를 해결하는 과정에 대한 설명을 정리하고자 한다.
- Monte Carlo methods
- rejection sampling
- MCMC (Markov Chain Monte Carlo)
- Marcov chain
- Metropolis-Hasting
- HMC (Hamiltonian Monte Carlo) 방법
- Rejection sampling
기존의 sample distribution은 튀어나온 구조 multiplicative constant해 distribution을 뽑기 어려워 이를 개선하기 위해 만든 sampling 방법이 rejection sampling이다.
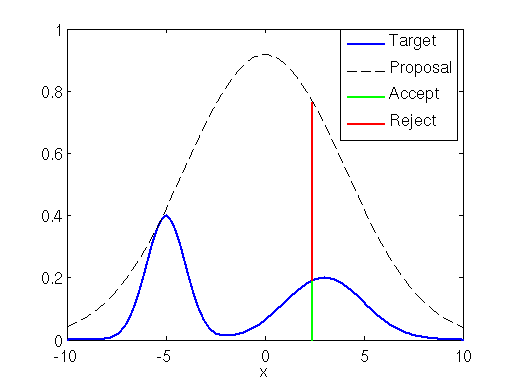
Rejection sampling을 이해하기 위해선 먼저 proposal distribution, target distribution에 대해 이해해야 한다.
p(x) = target distribution
q(x) = proposal distribution
p(x) target distribution은 말 그대로 내가 targeting하는 데이터에 대한 분포이고
q(x) proposal distribution는 target 분포와 가장 유사하면서 target 분포값들을 모두 포함한 uniform distribution이라 보면 된다.
위의 그림에서 볼 수 있듯이 선택한 데이터가 초록색 영역 accept부분에 있으면 채택하고, 그 외의 영역에 있는 값의 경우 거절하는 방식으로 sampling하는 것이다.
조금 더 자세히 수식을 통해 sampling하는 algorithm을 이해해보자,

1) 먼저 x값을 proposal distribution에서 선정한다.
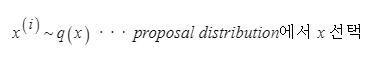
2) 임의의 u를 0에서 1사이의 숫자로 뽑는다.
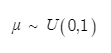
3) 이제 target distribution의 y값과 constant M을 곱한 proposal distribution y값을 서로 나눴을 때 만약 임의의 숫자 u가 작을 경우 채택하고, 클 경우 거절하는 식으로 target distribution에 근사한 sample들 값을 얻는다
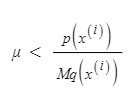
말로 쓰면 어렵지만 쉽게 보면 다음과 같다. Proposal distribution과 target distribution을 비교하여 target distribution 안에 들어오는 영역은 채택하고 그렇지 않은 영역은 거절하는 것이다.
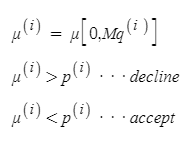
u의 식을 변형하여 보면 더 이해하기 쉬운데, Mq(x) propasal distribution을 곱하여 u를 0과 q(x)사이의 값을 선정하였을 때 만약 p(x) target distribution 안에 있으면 채택하고, 아니면 거절하는 것이다.