- 먼저 Bayesian Optimization은 뭘까?
머신러닝이나 딥러닝모델들의 parameter를 optimize하기 위해 여러 실험을 해야 되는데 이런 귀차니즘을 해결할 수 있는 알고리즘이 bayesian optimization이다. 최적화된 hyperparameter값을 찾아주는 알고리즘으로 최고의 성능을 도출해준다고 보면 된다.
(조금 더 구체적인 개념으로는 gaussian process regression 방법을 활용해 사후확률을 가장 잘 예측하도록 최적화하는 방법이다.)
본격적으로 Bayesian optimization을 알아보기 전에 관련된 기본용어 및 개념에 대해 알아보자!
보통 알려진 최적화된 Hyperparameter을 찾는 3가지 방법으로는 Grid Search, Random search, bayesian optimization 방법이 있다.
1) Grid Search : 무식하게 모두 대입해서 찾는 것
2) Random Search : Random한 sample을 search space에서 찾아서 대입
3) Bayesian optimization
Bayesian optimization에선 자주 등장하는 'black box'라는 용어가 있는데,
black box가 의미하는 바를 먼저 알아가보자
* black box:
Hyperparamter optimization은 직접 hyperparameter를 넣어서 optimize하는 것이고 automated machine learning은 모델을 hyperparameter에 최적화해서 제공하는 것이다.
이제 본격적으로 bayesian optimization에 대해 알아보자.
기본적으로 bayesian optimization은 exploration(새로운 것을 탐색)하는 것과 exploitation(현재 있는 것을 개선)의 balancing을 해 최적화를 찾아가는 것이다.
■ 그렇다면 bayesian optimization의 전체적인 탐색방법(algorithm 과정)은 어떻게 될까?

Surrogate model은 확률 모델을 선정하는 것으로 보면 되는데, 이 확률 모델을 활용하여 black box function을 수행해주는 역할을 한다.
surrogate model로 올 수 있는 모델들은
-
- Random forests
- Gaussian process regression
- Bayesian linear regression
- Nueral process, bayesian neural networks ...등이 있다.
먼저 surrogate model에 Input 값을 넣을 함수를 지정을 해주고 acquision function maiximization 과정을 통해 hyperparameter를 tuning한 최적의 값을 얻어 낼 수 있다.
[2] Acquisition function
Acquisition function의 역할은 surrogate model에 대하여 input(Train) data를 기반으로 다음 번 조사할 x값 x+1을 확률적으로 계산하여 추천해주는 함수이다.

위의 그림은 time point가 2일 때의 추정된 함수를 통해 나온 acquisiton function이다.
밑에 초록색 부분이 acquisition function으로 max값이 다음 x+1이 된다.
그림에서의 보라색 영역을 설명하자면 진한 실선이 목적 함수에 해당하고, 보라색 영역이 uncertainty를 포함한 영역이다. 즉 정답값을 포함한 신뢰도 영역이라 보면 되는데 평균과 표준편차로 결정된다.
⇒x+1이 결정되는 바는 평균와 σ2(x)이 가장 큰 값으로 결정되는데, uncertainty가 가장 높은 지점이 x+1이 된다고 볼 수 있다.
조금 더 acquisition function 구체적인 설명을 통해 이해해보자.
- 우선 Acquisition function의 종류들로는
- Probability of Improvement
- Expected Improvement
- GP Upper Confidence Bound(GP-UCB)
- Thompson sampling
등이 있고 이 중에서 expected Improvement가 가장 많이 쓰인다.
■ Probability of improvement를 통해 acquisition function이 만들어지는 과정을 보자
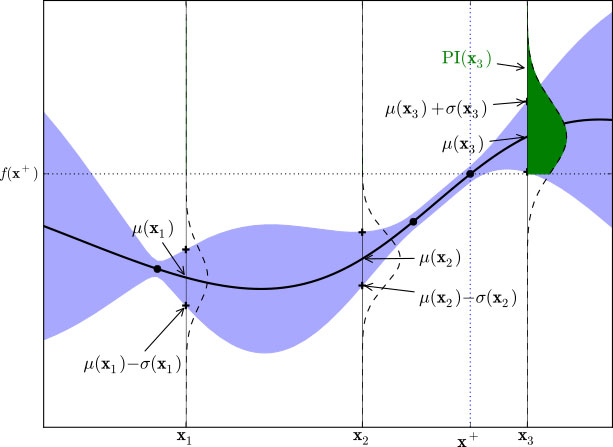
구체적인 개념 이해를 위해선 utility function을 이해하여야 하는데 너무 복잡하므로 직관적으로 이해하자면
그림상의 초록색 부분이 PI(Probability of improvent)함수에서 채택된 영역에 해당한다.
PI함수는 옆으로 보면 가우시안 분포 형태로 평균과 표준편차로 함수가 나타나지고 이제 초록색 영역이 채택되는 과정은 f(x+)보다 큰 영역값이 선정되어 채택된다.