오늘 내용은 대표적인 matrix decomposition에 해당하는 PCA, SVD을 이해하기 위한 기본 개념과 증명 과정에 대해 깊이 다루고자 한다.
관련 기본 개념들은 eigen decomposition, determinant 등이 있고 Eigen decomposition(고유값 분해)를 이해해해야 PCA를 이해 할 수 있기 때문에 꼭 알아야하는 개념 중 하나이다.
Matrix decomposition은 왜 사용해야 할까?

Matrix decomposition을 하는 이유는 행렬을 더 작은 구성 요소로 분해하여 계산을 더 쉽게 하거나 데이터의 중요한 특성을 추출하기 위해서 사용한다. 행렬 분해를 통해 우리는 데이터 차원을 축소 할 수 있을 뿐만 아니라 clustering, 중요한 feature 정보 추출, 패턴 인식 등등 다양하게 쓸 수 있다.
Eigen decomposition

Eigen decomposition은
정사각행렬을 고유값(eigenvalue)과 고유벡터(eigenvector)로 분해하는 방법이다.
고유값은 determinant를 통해 얻을 수 있는데
determinant의 개념은,
Determinant
고등학교 때 배운 determinant은 determinant(A)를 통해 역행렬을 구할 때 사용하였는데
이 역행렬 개념을 통해 행렬의 계산에 이 속성이 많이 사용된다.
행렬에서는 determinant는 공간을 의미한다. 행렬의 volume값을 측정할 수 있는 수단이다.
PCA는 우리가 정말 흔히 쓰지만 어떤 원리로 계산되는지 원리는 잘 모른채 사용할 때가 많다.
나도 처음 배울 땐 PCA가 한번에 이해가 되지 않았다, 다방면의 각도로 PCA를 이해하고
PCA를 이해하기 위해선 orthogonal, eigenvalue, eigenvector 용어에 익숙해 져야한다.
PCA(Principal Component Ananlysis)

PCA 결과에서 잘 보이는 PC1, PC2는 데이터를 가장 잘 표현하는 축(70%가량)이 PC1, PC2(11~15%가량)는 데이터를 표현한 축을 의미한다.
그렇다면 PCA는 어떤 과정을 통해 중심축을 얻게 되는 것일까?
이 중심축을 구하는 과정은 covariance matrix를 계산하는 것인데
(covariance, 공분산은 두 변수간의 상관관계를 의미한다)
PCA에서 covariance matrix를 구하는 이유는
데이터가 어느 축으로 많이 퍼져 있는가를 알기 위해서인데,
이 matrix 데이터와 데이터간의 상관관계를 계산하여 가장 설명하기 좋은 축(방향)이 무엇인지 찾는데 쓰인다.
Covariance matrix: λ1 A1 AT1 + λ2 A2 AT2 + ... + λn An ATn
위의 식 covariance matrix를 보면 여러개의 eigen decomposition의 합으로 이루어진 것을 볼 수 있다;
계산되는 과정은 다음과 같다.
1) Covariance matrix를 먼저 구하고
2) Eigen decomposition을 통해 Eigenvalue와 Eigenvector값을 구한다
3) Eigenvalue 크기 순으로 covariance matrix 내부 수식을 배열한다. 해당 순서가 PC1, PC2, PC3, ...가 되는 것이다.
여기까지가 PCA를 수학적으로 이해하는 것이고,
이제부터 PCA를 공간적인 접근으로 이해해보자

Z1, Z2, Zk라는 축이 있고,
이 셋중에 내 데이터를 가장 잘 표현하는 축을 찾는 과정이다.

어떤 기준으로 내 데이터가 이 축에서 표현이 잘 되었다고 할 수 있을까?
데이터의 점을 Z1, Z2, Zk 축에 대해 정사영(수직)을 내린다. (축 위에 찍혀 있는 점이 정사영을 한 점이다)
그리고 0을 기준으로 각 점까지의 거리들을 모두 곱한다.
그 곱이 가장 큰 것이 데이터를 가장 잘 표현한 축이라 할 수 있다.
마지막으로 정리하자면,
결국 Z1, Z2, Zk에 해당하는 축은 covariance matrix에서 eigenvector(방향성)을 의미한다.
covariance matrix에서 eigenvalue는 데이터를 표현하고 있는 수치이고 크면 클 수록 데이터를 잘 표현한다고 볼 수 있다.
SVD(Singlular value decomposition)
SVD는 모든 행렬 (정사각형, 직사각형 행렬)등등에 모두 쓰일 수 있는 matrix decomposition 방법중에 하나로 eigen decomposition 개념을 활용하여 얻어질 수 있다.
PCA와 SVD의 차이점은 PCA는 공분산행렬을 구한 뒤 고유값 분해를 할 수 있지만
SVD는 곧바로 고유값 분해를 할 수 있다.
이제 왜 SVD는 고유값 분해를 바로 할 수 있는지 그 계산 과정에 대해 보자
A 벡터를 SVD한 후의 결과이다.
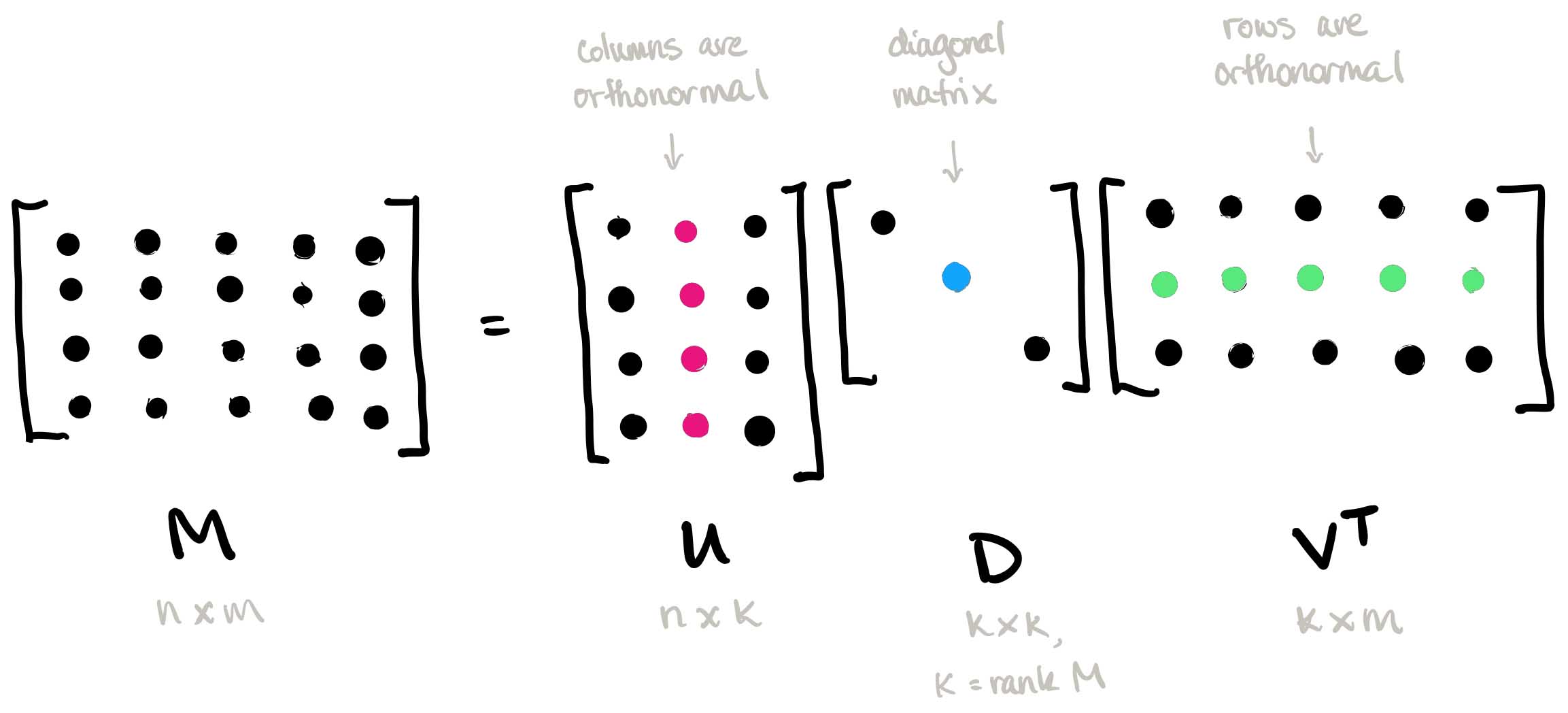

위의 식은 정사각형 행렬이 아닌 A(m*n) 를 정사각형 행렬로 만들기 위해선 AT(n*m) 를 곱하면 된다.
A의 행렬이 m*n 차원일때 Tranpose A는 n*m차원으로 둘이 곱하게 되는 경우 m*m 차원 정사각형이 되게 된다.
A AT와 ATA 은 정사각형 행렬이기 때문에 언제나 고유값 분해가 가능하다.
그러나 보통 SVD를 할 때 full SVD를 하진 않고 skinny SVD로 일부 U, V 행렬을 사용하여 근사행렬 값을 이용한다.